The order of a matrix is a fundamental concept in linear algebra that plays a crucial role in various mathematical applications. Understanding how to determine the order of a matrix not only enhances your mathematical skills but also builds a solid foundation for more advanced topics. In this article, we will dive deep into the definition, methods, and importance of determining the order of a matrix, ensuring you have a comprehensive grasp of this essential concept.
In the realm of mathematics, matrices are used to represent data, solve systems of equations, and perform transformations. Therefore, knowing how to determine the order of a matrix is essential for students, researchers, and professionals alike. From computer science to engineering, the applications of matrices are vast and varied.
This article will guide you through the steps to identify the order of a matrix, explaining key terms and providing practical examples. By the end of this article, you will have the knowledge and confidence to determine the order of any matrix you encounter.
Table of Contents
- What is a Matrix?
- Definition of Order
- How to Determine the Order of a Matrix
- Importance of Matrix Order
- Types of Matrices Based on Order
- Common Misconceptions
- Applications of Matrices in Real Life
- Conclusion
What is a Matrix?
A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. It is a crucial tool in mathematics and is often denoted by capital letters. Matrices serve various purposes, such as representing data sets, solving linear equations, and performing linear transformations.
For example, a matrix can be used to represent a system of equations, where each row corresponds to a single equation and each column corresponds to a variable. The elements within the matrix represent the coefficients of these variables.
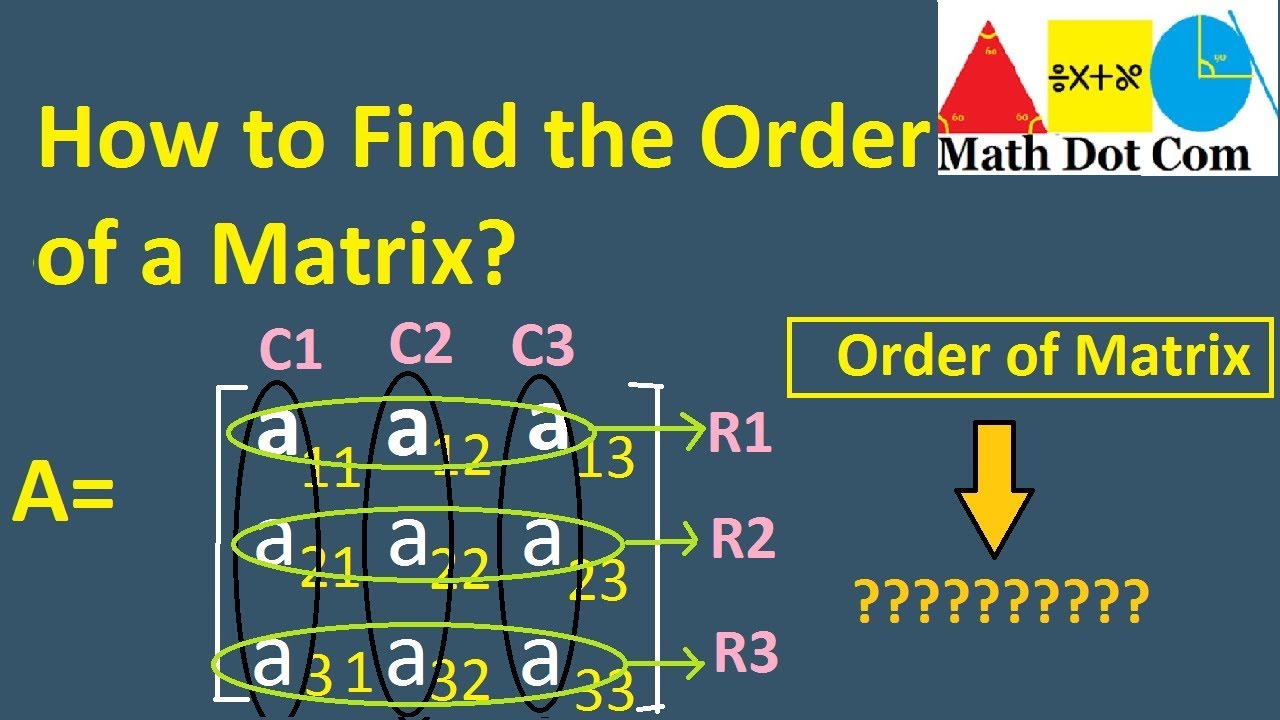
Definition of Order
The order of a matrix refers to the dimensions of the matrix, specifically the number of rows and columns it contains. It is usually expressed in the format 'm x n', where 'm' represents the number of rows and 'n' represents the number of columns. For instance, a matrix with 3 rows and 4 columns is said to be of order 3 x 4.
How to Determine the Order of a Matrix
Determining the order of a matrix is a straightforward process. Here are the steps to follow:
Counting Rows and Columns
- Identify the number of rows in the matrix.
- Identify the number of columns in the matrix.
- Express the order in the format 'm x n'.
For example, consider the following matrix:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
In this case, there are 2 rows and 3 columns, so the order of the matrix is 2 x 3.
Example of Determining Order
Let’s consider another example. Here is a matrix:
| 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 |
This matrix has 3 rows and 4 columns, making its order 3 x 4.
Importance of Matrix Order
Understanding the order of a matrix is essential for several reasons:
- Matrix Operations: Certain operations, such as addition and multiplication, require matrices to have compatible orders.
- Data Representation: The order of a matrix affects how data is represented and interpreted, particularly in fields like computer science and statistics.
- Problem Solving: Knowing the order helps in setting up and solving systems of equations efficiently.
Types of Matrices Based on Order
Matrices can be categorized based on their order:
- Square Matrix: A matrix where the number of rows equals the number of columns (e.g., 3 x 3).
- Rectangular Matrix: A matrix where the number of rows does not equal the number of columns (e.g., 2 x 3).
- Row Matrix: A matrix with only one row (e.g., 1 x n).
- Column Matrix: A matrix with only one column (e.g., m x 1).
Common Misconceptions
There are several misconceptions surrounding the order of matrices:
- All matrices are square: This is false; matrices can be rectangular as well.
- The order does not matter: The order is critical for performing matrix operations, and incompatible orders can lead to errors.
Applications of Matrices in Real Life
Matrices are widely used in various fields, including:
- Computer Graphics: Matrices are used to perform transformations such as rotation, scaling, and translation of images.
- Economics: Matrices can represent and solve systems of linear equations in economic models.
- Engineering: Engineers use matrices for structural analysis and designing complex systems.
Conclusion
In summary, determining the order of a matrix is a fundamental skill in linear algebra that unlocks the door to various mathematical applications. By understanding the definition, methods, and importance of matrix order, you can enhance your problem-solving capabilities and apply this knowledge in real-world scenarios. If you found this article helpful, please leave a comment, share it with others, or explore more articles on our site!
Call to Action
Now that you have a better understanding of how to determine the order of a matrix, why not test your knowledge? Try finding the order of different matrices you encounter in your studies or work. Feel free to share your findings in the comments below!
You Might Also Like
City Walk Restaurants: Discover The Best Dining ExperiencesUnveiling The Mystery Of The Annabelle Doll: A Deep Dive Into The Haunted Legend
Costner Fires De Niro: The Untold Story Behind The Controversy
Exploring Steven Yeun's Age: A Journey Through Time And Talent
Booty Lifting Shapewear: The Ultimate Guide To Achieve A Perfect Silhouette
Article Recommendations
- Is Zach Top Married
- Celebrities With Essential Thrombocythemia
- Norissa Valdez Leaks
- Dafne Keen Leaked
- Latest Sexy Videos
- Vegamovies Adult
- Was John Pinette Married
- Zoe Moore Leak
- Is Mark Levin Sick
- Dafne Keen Nude Video